Scribe Post - 05/30/06
Sequences
The Scribe Post - May 30, 2006
- We only have one class today, since Caitlin wasn't in our class, Stephanie decided that I should go instead but anyways. Here is what we did.......
Mr. K directly putted up 4 Sequences while the announcers are speaking. He asked.
Find the next three Terms.....


The Scribe Post - May 30, 2006
- We only have one class today, since Caitlin wasn't in our class, Stephanie decided that I should go instead but anyways. Here is what we did.......
Mr. K directly putted up 4 Sequences while the announcers are speaking. He asked.
Find the next three Terms.....
4, 7, 10, 13, ?, ?, ?
3, 6, 12, 24, ?, ?, ?
32, 16, 8, 4, ?, ?, ?
2, 3, 5, 8,12, ?, ?, ?
The Answers.....
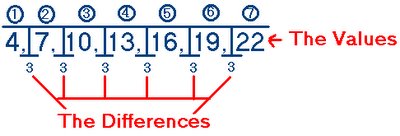
4, 7, 10, 13, 16, 19, 22
3, 6, 12, 24, 48, 96, 192
32, 16, 8, 4, 2, 1, 1/2
2, 3, 5, 8, 12, 17, 23, 30
32, 16, 8, 4, 2, 1, 1/2
2, 3, 5, 8, 12, 17, 23, 30
How did we find out?
It is actually easy to find out, what is the next number of these values, IF YOU HAVE COMMON SENSE; we're not actually talking common sense in here, but I would like to say we're talking about math and here how it goes.
We see in 4, 7, 10, 13, 16, 19, 22 this values have all the same differences, and the difference between this numbers is THREE ( 3 ). It is easy to see that 3 is the difference, there is also another way to do it.
One of the way we can solve the number is by 3 (The Differences) multiply by the numbers right up the value and add 1.

The right equation for this Sequence is tn = n3 + 1 This is the RULE.
If you would to find out what is the next term without finding the TERM BEFORE THAT, this is what we called the RECURSIVE DEFINITION. The other definition for that is ..... Do the same thing to get the next answer is the ReCursive Definition.
For EXAMPLE, if you would like to find the 7th term without finding out what is the 5th, and the 6th terms. The equation for that is........

We need to put in the First term then we add the Number of Columns then minus 1 from it since there is only 6 in between and in between that's the differences and the Difference for this value is 3.
TO SOLVE THE EQUATION BY FINDING THE TERM 7...this is how is goes.
T7 = 4 + (7-1) 3
--- = 4 + (6) 3
--- = 4 + 18
--- = 22
( The SEQUENCE THAT HAVE A COMMON DIFFRENCE IS WHAT WE CALLED ARITHMETIC, and one example is right above*)
FOR THE NEXT SEQUENCE.
3, 6, 12, 24, 48, 96, 192
(This sequence is what we called GEOMETRIC, by having COMMON RATIOS in all the values*)
This is how we solve the equation, by finding the term without looking for the number before that value.

Tn = the term you are looking for
T1 = the first term
r = the ratio
n-1= the number of columns minus 1
T7 = 3 (2)^7-1
T7 = 3 (2)^6
T7 = 3 (64)
T7 = 192
The last two Sequence are also GEOMETRIC, because they don't have a common differences.
Then later on that period Mr. K told us about the Implicit and Explicit.
Implicit is a cuirrent inside suggestion
Explicit is a high current outside.
There is one more way we can find it, the LAST ONE IS IN OUR CALCULATOR. First we need to check if our mode is in SEQUENCE, so CLICK MODE, Go to the 4th row then choose SEQ.Then we enter our information in our Y= screen, and then we need to check our window for a better view.
To generate:
Go Second Quit
Enter in your calculator:
u by 2nd, 7 the bracets (First Term, and the up to what term would you like to see)
Then we store it in our L1.
MR.K also SAID THAT ADD UP SEQUENCES IS CALLED SERIES.
I don't know if I'm doing good at this scribe post this time, damn I shouldn't have wait for a day to fix this up now my memory is kind of loosing it.